Статистическая теория каналов связи

Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru

Данная статья имеет целью познакомить с терминологией и математическими основами статистической теории передачи данных. Именно на этой математической основе зиждятся приведенные выше теоремы Шеннона и Найквиста. Статья является компиляцией из нескольких источников (Ю.В.Прохоров, Ю.А.Розанов "Теория вероятностей. Основные понятия, предельные теоремы, случайные процессы" Наука, М. 1967; Л.Ф. Куликовский, В.В.Мотов, "Теоретические основы информационных процессов", Высшая школа, 1987; Р. Галлагер "Теория информации и надежная связь" Советское радио, 1974 и др.). Материалы, предлагаемые здесь не могут считаться исчерпывающими и призваны быть поводом для более углубленного изучения по существующим монографиям.

Канал связи предназначен для транспортировки сообщений. Математическая модель канала связи описывается некоторой совокупностью Х1 элементов х1 (X1 = {x11, x12,, …x1j}), называемых сигналами на входе канала, совокупностью Х2 элементов х2 (x2 = {x21, x22,, …x2k}), называемых выходными сигналами, и условными распределениями вероятностей p2=p2(a2 |x1) в пространстве x2 выходных сигналов x2. Если посланный сигнал (сигнал на входе) есть х1, то с вероятностью P2=P2(A2|x1) на выходе канала будет принят сигнал х2 из некоторого множества A2 М Х2 (распределения задают вероятности того или иного искажения посланного сигнала х1). Совокупность всех возможных сообщений обозначим символом x0. Предполагается, что каждое из сообщений x0О X0 может поступать с определенной вероятностью. То есть, в пространстве X0 имеется определенное распределение вероятностей P0=P0(A0 ).

Сообщения х0 не могут быть переданы по каналу связи непосредственно, для их пересылки используются сигналы x1О X1. Кодирование сообщений х0 в сигналы х1 описывается при помощи условного распределения вероятностей P1=P1(A1 |x0). Если поступает сообщение х0, то с вероятностью P1=P1(A1|x0) будет послан один из сигналов х1, входящих в множество A1 М Х1 (условные распределения P1(A1|x0) учитывают возможные искажения при кодировании сообщений).
Аналогичным образом описывается декодирование принимаемых сигналов х2 в сообщения x3. Оно задается условным распределением вероятностей P3=P3(A3|x2) на пространстве Х3 сообщений х3, принимаемых на выходе канала связи.

На вход канала связи поступает случайное сообщение x0 с заданным распределением вероятностей P0=P0(A0). При его поступлении передается сигнал x1, распределение вероятностей которого задается правилом кодирования P1=P1(A1|x0):

P{x2 О A2|x0, x1} = P2(A2|x1)

Принятый сигнал x2 декодируется, в результате чего получается сообщение x3:

P{x3 О A3|x0, x1, x2} = P3(A3| x2)

Последовательность x0 ® x1 ® x 2 ® x3 является марковской. При любых правилах кодирования и декодирования описанного типа имеет место неравенство:

I(x0,x3) Ј I(x1, x2),

где I(x0, x3) - количество информации о x0 в принятом сообщении x3, I(x1, x2) - количество информации о x1 в принятом сигнале x2.

Предположим, что распределение вероятности входного сигнала x1 не может быть произвольным и ограничено определенными требованиями, например, оно должно принадлежать классу W. Величина C = sup I(( x1 , x2) , где верхняя грань берется по всем возможным распределениям P1 О W, называется емкостью канала и характеризует максимальное количество информации, которое может быть передано по данному каналу связи (теорема Шеннона).

Предположим далее, что передача сообщений x0 ® x3 должна удовлетворять определенным требованиям точности, например, совместное распределение вероятностей Px0 x1 передаваемого и принимаемого сообщений x0 и x3 должно принадлежать некоторому классу V. Величина H= inf I( x0 x3), где нижняя грань берется по всем возможным распределениям Px0 x3 О V, характеризует минимальное количество информации, которое должно заключать в себе принимаемое сообщение x3 о x0, чтобы было выполнено условие точности передачи. Величина H называется энтропией источника сообщений.

Если возможна передача x0 ® x1 ® x2 ® x3 с соблюдением требований V и W, то есть существуют соответствующие способы кодирования и декодирования (существуют условные распределения P1, P2 и P3), то H Ј С.



Для выполнения этого неравенства передача является возможной, т.е. возможна передача последовательно поступающих сообщений

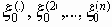
Предположим, что совокупность Х0 всех возможных сообщений х0 является дискретной (имеется не более чем счетное число различных сообщений x0, поступающих с соответствующими вероятностями P0(x0), x0 О X0) и условие точности передачи v состоит в том, что принимаемое сообщение x3 должно просто совпадать с переданным сообщением x3 = x0 с вероятностью 1. Тогда



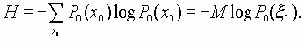
Предположим далее, что имеется лишь конечное число N различных входных сигналов х1 и нет никаких ограничений на вероятности P{ x1 = x1}, x1   О  X1. Кроме того, предположим, что передаваемые сигналы принимаются без искажений, то есть с вероятностью 1 x2= x1. Тогда емкость канала выражается формулой C = log2N, т.е. передаваемое количество информации I(x1, x 2 ) будет максимальным в том случае, когда сигналы x1 О X1 равновероятны.

Если сообщения поступают независимо друг от друга, то количество информации, которое несет группа сообщений есть


группа сообщений, поступающая на кодирование с вероятностью


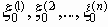
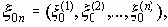
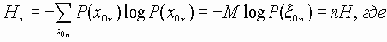
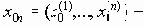
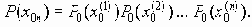
Пусть H<C, положим также d=(1/2)(C-H). Согласно закону больших чисел, примененному к последовательности независимых и одинаково распределенных случайных величин


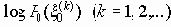
с математическим ожиданием

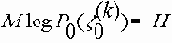
для любого e >0 найдется такое n(e), что при всех n і n(e )

P{-H-d Ј (1/n)logP( x 0n) Ј H+d } і 1-e, где


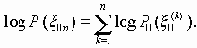
Полученное неравенство говорит о том, что все группы сообщений х0n можно разбить на два класса. К первому классу относятся высоковероятные сообщения х0n, для которых P(x0n) і 2-n(H+d ) и количество которых Mn не больше чем 2n(H+d ):

Mn Ј 2n(H+d )

Ко второму классу относятся все остальные маловероятные сообщения х0n:
.

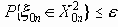
Каждую группу высоковероятных сообщений х0n можно в принципе передать, закодировав ее соответствующей комбинацией сигналов . Число всевозможных комбинаций такого вида есть Nn=2nC, и видно, что Mn<Nn. Имеется Nn различных сигналов x1n, с помощью которых можно закодировать и передать безошибочно все Mn высоковероятных сообщений x0n Если в дополнение к этому при поступлении любого маловероятного сообщения x0n передавать некоторый один и тот же сигнал (отличный от сигналов, при помощи которых передаются высоковероятные сообщения x0n , то с вероятностью, не меньшей чем 1-e, на выходе канала связи будет приниматься последовательность :



.

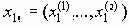
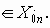
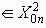
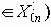
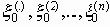
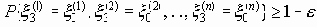
При выполнении неравенства H < C оказывается возможной передача достаточно длинных сообщений с той оговоркой, что с вероятностью e (e - наперед заданное сколь угодно малое положительное число) может быть допущена ошибка. Имеется целое семейство каналов связи и источников сообщений, зависящих от параметра n.

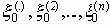
Количество информации I(x0, x3) для абстрактных случайных величин x0 и x3 со значениями в пространствах Х0 и Х3 может быть записано в виде:

I(x0, x 3) = Mi(x0, x3), где


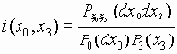
- информационная плотность. Последовательность пар (x0n, x3n) называется информационно устойчивой, если при n ® Ґ

I(x0, x3) ® Ґ и

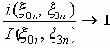
(по вероятности)

Рассмотренная выше последовательность (x0n, x3n), x3n= x0n поступающих сообщений x 0n =( ) обладает свойством информационной устойчивости, что в конечном счете и определило возможность передачи сообщений x 0n с точностью до e. Этот факт допускает широкое обобщение. Например, если Сn - пропускная способность канала
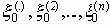
x1n® x 2n, Hn - минимальное количество информации, необходимое для соблюдения требуемой точности передачи x0n ® x 3n, причем


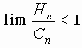
(при n ® Ґ ),

и существуют информационно устойчивые последовательности пар (x0n, x3n) и (x1n, x2n), для которых одновременно



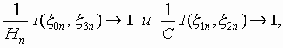
то при весьма широких предположениях для любого наперед заданного e >0 существует такое n(e), что по всем каналам связи с параметром n і n(e) возможна передача с точностью до e.


Содержание раздела

---